CF406D Hill Climbing

本题与 Little Chris 无关，讨论的是“爬山人”（hill climbers）。Chris 绝对不是其中之一。 有 $n$ 座山排成一排，每座山可以视作一条竖直线段的一端在地面上。这些山从左到右依次编号为 $1$ 到 $n$。第 $i$ 座山在 $x_i$ 位置，高度为 $y_i$。对于任意两座山 $a$ 和 $b$，若从 $b$ 的顶部能看到 $a$ 的顶部，则用绳子连接这两座山的顶部。正式地说，若连接这两座山顶的线段不会与其它任何一座山的线段相交或相切，则这两座山的顶端可连接绳子。通过这些绳索，爬山人可以从一座山移动到另一座山。 有 $m$ 支登山小队，每队正好有两名成员。第 $i$ 支小队的两名登山者分别位于第 $a_i$ 座与第 $b_i$ 座山的顶部。他们想在某座山顶会合。两名登山者的移动规则如下： 1. 如果登山者当前就在对方已经位于（或未来会抵达的）山顶，则这个登山者停在该山顶； 2. 否则，他会选择从当前位置通过绳子可到达且靠右的山顶（即可达的最右边的山顶），然后继续上述过程（他可以攀爬比当前山矮的山顶）。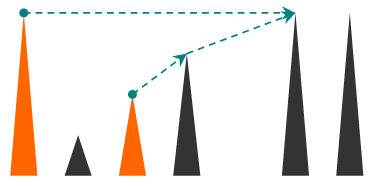  对于每支登山小队，输出这两名成员最终汇合的山顶编号！

第一行输入一个整数 $n$（$1 \leq n \leq 10^{5}$），表示山的数量。接下来的 $n$ 行，每行包含两个用空格分隔的整数 $x_i$、$y_i$（$1 \leq x_i \leq 10^{7}$；$1 \leq y_i \leq 10^{11}$），表示第 $i$ 座山的位置和高度。山顶的信息按 $x_i$ 严格递增给出，即如果 $i < j$，那么 $x_i < x_j$。 接下来一行输入一个整数 $m$（$1 \leq m \leq 10^{5}$），表示队伍数量。接下来的 $m$ 行，每行包含两个用空格分隔的整数 $a_i$、$b_i$（$1 \leq a_i, b_i \leq n$），表示第 $i$ 支队伍的两名成员所在地的山的编号。可能出现 $a_i = b_i$。

在一行输出 $m$ 个用空格分隔的整数，第 $i$ 个整数表示第 $i$ 支队伍两名成员最终会合的山顶编号。

由 ChatGPT 5 翻译