CF435E Special Graph

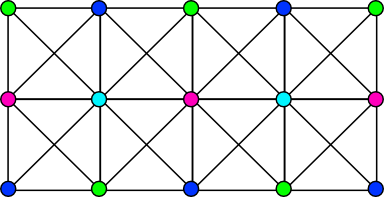
在本题中，你需要处理一个 $n \times m$ 的网格图。该图的顶点是 $n \times m$ 网格的每个节点。图的边包括所有单元格的边和对角线。 下图展示了一个 $3 \times 5$ 的网格图。黑色线段表示图的边，彩色圆圈表示图的顶点。图中的顶点被着色是有原因的：这个染色是 $3 \times 5$ 网格图的一个合法四色定点染色。一个合法的图染色要求每个顶点都被染色，并且任意通过一条边直接相连的两个顶点不能染成相同的颜色。  给定一个 $n \times m$ 的网格图以及该图部分顶点的颜色。请找出一种方法，为未染色的顶点染上四种颜色，使得最终结果是一个合法的顶点染色。如果不存在这样的合法染色，请输出不存在解。

第一行包含两个整数 $n$ 和 $m$，表示网格的行数和列数，满足 $2 \leq n, m \leq 1000$。 接下来的 $n$ 行，每行包含 $m$ 个字符，表示给定的网格。每个字符要么是“0”、“1”、“2”、“3”或“4”。字符“0”表示对应顶点未染色，其他字符表示该顶点的颜色。 所有可用颜色编号为 $1$ 到 $4$。

如果无法获得一个合法的顶点染色，输出一行 0。 否则，输出最终的 $n \times m$ 染色图。输出格式与输入相同。 如果存在多种答案，输出任意一种均可。

第一个样例的答案见图示（1 表示绿色，2 表示蓝色，3 表示深蓝色，4 表示粉色）。 第二个样例存在 $4!$ 种答案，每种都被认为是合法答案。 第三个样例中，有两个用相同颜色的顶点通过一条边相连。此时无法获得合法的顶点染色。 由 ChatGPT 5 翻译