CF437B The Child and Set

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite set of Picks. Fortunately, Picks remembers something about his set $ S $ : - its elements were distinct integers from $ 1 $ to $ limit $ ; - the value of 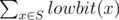 was equal to $ sum $ ; here $ lowbit(x) $ equals $ 2^{k} $ where $ k $ is the position of the first one in the binary representation of $ x $ . For example, $ lowbit(10010_{2})=10_{2},lowbit(10001_{2})=1_{2},lowbit(10000_{2})=10000_{2} $ (binary representation). Can you help Picks and find any set $ S $ , that satisfies all the above conditions?

The first line contains two integers: $ sum,limit $ $ (1

In the first line print an integer $ n $ $ (1

In sample test 1: $ lowbit(4)=4,lowbit(5)=1,4+1=5 $ . In sample test 2: $ lowbit(1)=1,lowbit(2)=2,lowbit(3)=1,1+2+1=4 $ .