CF437E The Child and Polygon
Description
This time our child has a simple polygon. He has to find the number of ways to split the polygon into non-degenerate triangles, each way must satisfy the following requirements:
- each vertex of each triangle is one of the polygon vertex;
- each side of the polygon must be the side of exactly one triangle;
- the area of intersection of every two triangles equals to zero, and the sum of all areas of triangles equals to the area of the polygon;
- each triangle must be completely inside the polygon;
- each side of each triangle must contain exactly two vertices of the polygon.
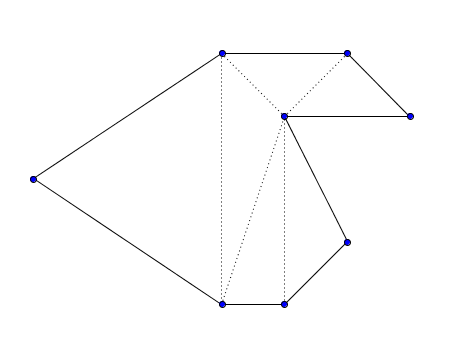
The picture below depicts an example of a correct splitting.
Please, help the child. Calculate the described number of ways modulo $ 1000000007 $ $ (10^{9}+7) $ for him.
Input Format
The first line contains one integer $ n $ $ (3
Output Format
Output the number of ways modulo $ 1000000007 $ $ (10^{9}+7) $ .
Explanation/Hint
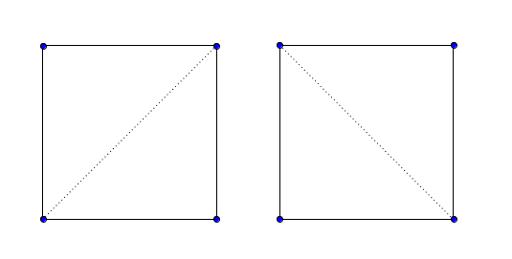
In the first sample, there are two possible splittings:
In the second sample, there are only one possible splitting: