CF437E The Child and Polygon
题目描述
这一次,小朋友有一个简单多边形。他需要计算将该多边形划分为若干个非退化三角形的方案数。每种方案必须满足以下要求:
- 每个三角形的每个顶点都必须是多边形的顶点;
- 多边形的每条边必须且仅能作为某个三角形的边;
- 每两个三角形的交集面积为零,所有三角形的面积总和等于多边形面积;
- 每个三角形必须完全位于多边形内部;
- 每个三角形的每条边必须恰有两个多边形的顶点。
下图展示了一个合法的划分示例:
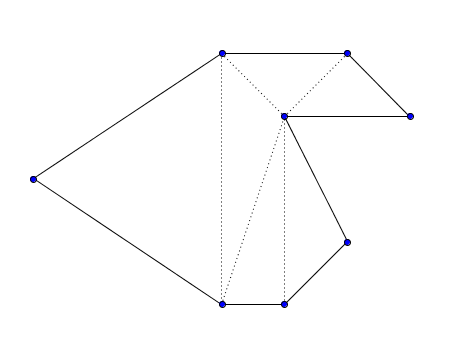
请帮帮小朋友,计算满足描述的划分方案数,结果对 $1000000007$ ($10^{9} + 7$)取模。
输入格式
第一行包含一个整数 $n$($3 \leq n \leq 200$),表示多边形的顶点数量。接下来 $n$ 行,每行两个整数,表示多边形的第 $i$ 个顶点的坐标 $x_i, y_i$($|x_i|, |y_i| \leq 10^{7}$),顶点按照顺时针或逆时针顺序给出。
保证该多边形是简单多边形。
输出格式
输出满足条件的划分方案数,对 $1000000007$($10^9 + 7$)取模。
说明/提示
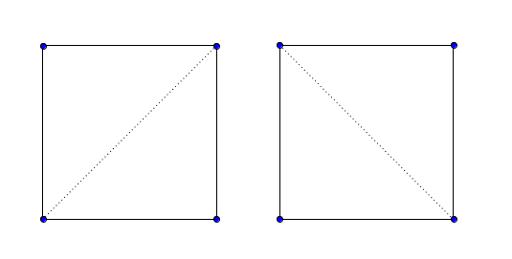
在第一个样例中,有两种可能的划分方式:
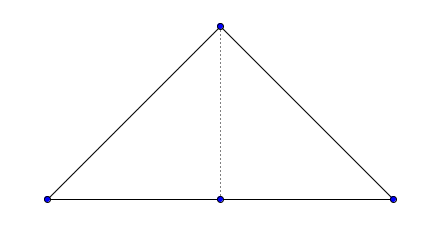
在第二个样例中,只有一种划分方式:
由 ChatGPT 5 翻译