CF438E The Child and Binary Tree

Our child likes computer science very much, especially he likes binary trees. Consider the sequence of $ n $ distinct positive integers: $ c_{1},c_{2},...,c_{n} $ . The child calls a vertex-weighted rooted binary tree good if and only if for every vertex $ v $ , the weight of $ v $ is in the set $ {c_{1},c_{2},...,c_{n}} $ . Also our child thinks that the weight of a vertex-weighted tree is the sum of all vertices' weights. Given an integer $ m $ , can you for all $ s $ $ (1

The first line contains two integers $ n,m $ $ (1

Print $ m $ lines, each line containing a single integer. The $ i $ -th line must contain the number of good vertex-weighted rooted binary trees whose weight exactly equal to $ i $ . Print the answers modulo $ 998244353 $ ( $ 7×17×2^{23}+1 $ , a prime number).

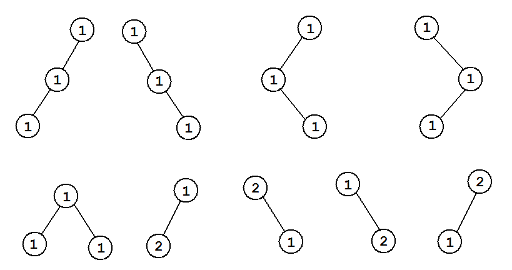
In the first example, there are $ 9 $ good vertex-weighted rooted binary trees whose weight exactly equal to $ 3 $ :