CF438E The Child and Binary Tree

我们的孩子非常喜欢计算机科学，尤其喜欢二叉树。 考虑一个由 $n$ 个互不相同的正整数组成的数列：$c_{1},c_{2},\ldots,c_{n}$。孩子称某个点权二叉树为“好”的二叉树，当且仅当对于每个结点 $v$，$v$ 的权值属于集合 $\{c_{1},c_{2},\ldots,c_{n}\}$。此外，我们的孩子认为一棵点权二叉树的权值等于所有结点权值之和。 给定整数 $m$，你能否对于所有 $s$（$1 \leq s \leq m$）计算出权值恰好为 $s$ 的“好”的有根二叉树的数量？请参考样例理解哪些树被认为是不同的。 我们只需要你输出答案对 $998244353$ 取模后的结果（$7 \times 17 \times 2^{23} + 1$，是一个质数）。

第一行包含两个整数 $n, m$，满足 $1 \leq n \leq 10^{5}$，$1 \leq m \leq 10^{5}$。 第二行包含 $n$ 个两两不同的正整数 $c_1, c_2, \ldots, c_n$，$1 \leq c_i \leq 10^{5}$。

输出 $m$ 行，每行包含一个整数。第 $i$ 行输出权值恰好为 $i$ 的“好”的有根二叉树的数量，对 $998244353$ 取模。

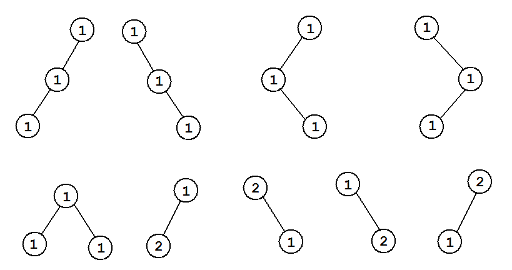
在第一个样例中，权值恰好为 $3$ 的“好”的有根二叉树共有 $9$ 种：  由 ChatGPT 5 翻译