CF441C Valera and Tubes

Valera has got a rectangle table consisting of $ n $ rows and $ m $ columns. Valera numbered the table rows starting from one, from top to bottom and the columns – starting from one, from left to right. We will represent cell that is on the intersection of row $ x $ and column $ y $ by a pair of integers $ (x,y) $ . Valera wants to place exactly $ k $ tubes on his rectangle table. A tube is such sequence of table cells $ (x_{1},y_{1}) $ , $ (x_{2},y_{2}) $ , $ ... $ , $ (x_{r},y_{r}) $ , that: - $ r>=2 $ ; - for any integer $ i $ $ (1

The first line contains three space-separated integers $ n,m,k $ ( $ 2

Print $ k $ lines. In the $ i $ -th line print the description of the $ i $ -th tube: first print integer $ r_{i} $ (the number of tube cells), then print $ 2r_{i} $ integers $ x_{i1},y_{i1},x_{i2},y_{i2},...,x_{iri},y_{iri} $ (the sequence of table cells). If there are multiple solutions, you can print any of them. It is guaranteed that at least one solution exists.

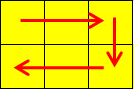
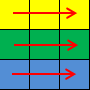Picture for the first sample: Picture for the second sample: