CF442D Adam and Tree
题目描述
树指的是一种无向连通图且满足任意两个点间不存在两条不同的简单路径;
彩色树指的是一种每条边都有一种颜色的树,并且同一种颜色的边集一定形成一条路径。
对于彩色树上的任意一个点 $u$,定义其权值 $w(u)$ 为 $u$ 至根节点(即 1 号点)的路径上所有边的颜色种类数。
彩色树会生长,初始时树中仅有根节点 1 号点,每个时刻都会有一个新节点长出来。每个时刻(包括初始时刻),你需要决定每条边的颜色,在满足彩色树的定义的前提下,使这个时刻树中节点权值的最大值最小。
输入格式
第一行一个正整数 $n\ (1\leq n\leq 10^6)$。
第二行 $n$ 个正整数,第 $i$ 个正整数 $p_i\ (1\leq p_i\leq i)$,表示第 $i$ 时刻加入点 $i+1$ 且其父亲为 $p_i$。
输出格式
一行,共 $n$ 个正整数,第 $i$ 个数表示时刻 $i$(即加入点 $i+1$ 后)的答案。
说明/提示
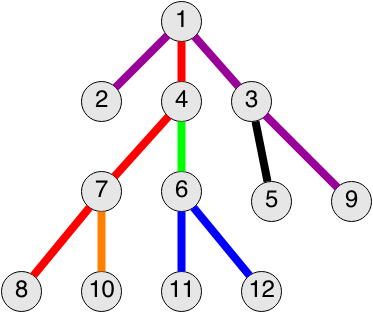
The figure below shows one of the possible variants to paint a tree from the sample at the last moment. The cost of the vertexes with numbers 11 and 12 equals 3.