CF449A Jzzhu and Chocolate

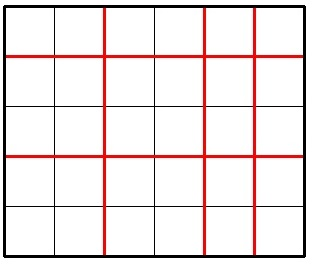Jzzhu 有一块大的矩形巧克力，包含 $n \times m$ 个单位小方格。他想要对这块巧克力恰好切割 $k$ 次。每次切割需要满足以下要求： - 每次切割必须是直线（水平或垂直）； - 每次切割必须沿着单位方格的边进行（不允许把任何一个单位巧克力格子切开）； - 每次切割都必须在整个巧克力内部，并且所有的切割操作必须彼此不同。 下图展示了将 $5 \times 6$ 的巧克力切割 $5$ 次的一种可能方式。 假设 Jzzhu 已经完成了 $k$ 次切割，这块大的巧克力被分成了若干块。请考虑巧克力中面积最小的那一块，Jzzhu 希望这块巧克力的面积尽可能大。请你计算：用恰好 $k$ 次切割后，最小区域的最大可能面积是多少？巧克力块的面积指其包含的单位方格数。

一行包含三个整数 $n,m,k$，表示巧克力的行数、列数和切割次数，满足 $1 \leq n, m \leq 10^{9}$，$1 \leq k \leq 2 \times 10^{9}$。

输出一个整数，表示答案。如果无法对巧克力进行 $k$ 次有效切割，则输出 $-1$。

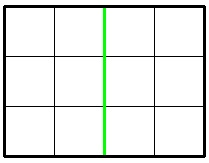
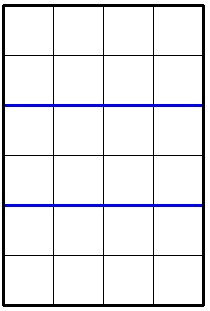
在第一个样例中，Jzzhu 可以按照下图把巧克力分割：  在第二个样例中，最优的分割如下图所示：  在第三个样例中，不可能将 $2 \times 3$ 的巧克力切割 $4$ 次。 由 ChatGPT 5 翻译