CF451A Game With Sticks

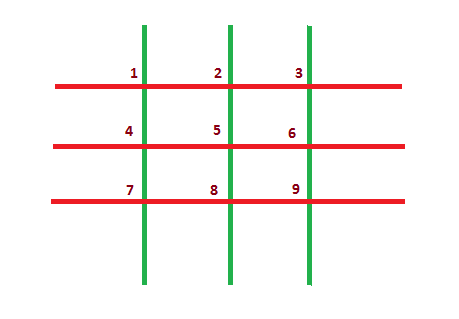
在 IOI 2014 上获得金牌和银牌后，Akshat 与 Malvika 想要娱乐一下。现在他们正在一张由 $n$ 根水平木棍和 $m$ 根竖直木棍组成的网格上玩游戏。 交点是指由一根水平木棍和一根竖直木棍交汇而成的点。 在下图所示的网格中，$n=3$，$m=3$。总共有 $n + m = 6$ 根木棍（红色为水平木棍，绿色为竖直木棍）。共有 $n \cdot m = 9$ 个交点，编号从 $1$ 到 $9$。  游戏的规则非常简单。两名玩家轮流行动。Akshat 获得金牌，因此由他先手。在他的回合，玩家必须选择任意一个尚未被移除的交点，并从网格上移除所有经过该点的木棍。若在某名玩家的回合中，他无法选择任何交点（即网格上已无交点），则该玩家输掉游戏。 假设两位玩家都采取最优策略。请你判断谁将会获胜。

输入的第一行为两个用空格分隔的整数 $n$ 和 $m$（$1 \leq n, m \leq 100$）。

输出一行，内容为 "Akshat" 或 "Malvika"（不含引号），表示该游戏的获胜者。

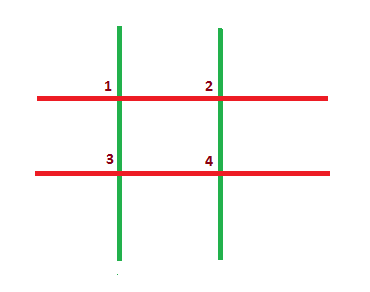
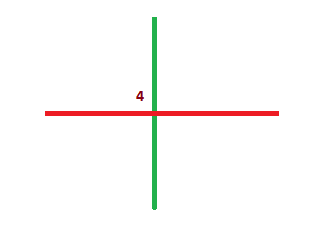
样例一的解释： 网格上有 $4$ 个交点，编号为 $1$ 至 $4$。  如果 Akshat 选择交点 $1$，那么他会移除两根木棍（$1-2$ 和 $1-3$）。此时网格如下所示。  现在只剩下一个交点（即 $4$）。Malvika 必须选择该交点并移除仅剩的两根木棍。她走完后，网格将变为空。 在空网格上，Akshat 无法继续行动，因此他输掉比赛。 由于网格上的所有 $4$ 个交点完全等价，无论 Akshat 选择哪一个交点，他都会输掉比赛。 由 ChatGPT 5 翻译