CF457A Golden System

### 完整题意 Piegirl 已经对二进制、十进制以及其他整数计数系统感到厌倦。最近她发现了关于数字 $q=\frac{\sqrt5+1}{2}$ 的一些有趣的性质，特别是当 $q^2=q+1$ 时，并且她认为这将为她的独特的新系统打下良好基础。她管这叫“黄金系统”。在黄金系统中，数字是包含 $0$ 与 $1$ 的非空字符串，表达式 $a_0a_1\dots a_n$ 的十进制值为 $\sum_{i=0}^{n}a_i\times q^{i-1}$。 很快她就发现这个系统不具有基础整数计数系统的性质，并且有些操作无法在这上面执行。她无法想出一种快速比较两个数的方法，于是来向你求助。 给出两个用黄金系统表示的数，比较哪个数更大。

输入由两行组成。每行为一个只包含 $0$ 和 $1$ 的字符串，每个字符串长度不超过 $10^5$。

输出只包含一个字符。如果第一个数更大，则输出 `>`，如果第二个数更大，则输出 `

In the first example first number equals to 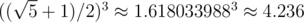, while second number is approximately $ 1.618033988^{2}+1.618033988+1≈5.236 $ , which is clearly a bigger number. In the second example numbers are equal. Each of them is $ ≈2.618 $ .