CF466C Number of Ways
题目描述
给定一个由 $n$ 个整数构成的数组 $a[1],a[2],...,a[n]$。请计算有多少种方法可以将这个数组分割为三个连续的部分,使得每一部分的元素之和都相等。
更正式地,你需要找出有多少对下标 $i,j$ 满足 $2 \leq i \leq j \leq n-1$,并且下列条件成立:
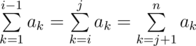。
输入格式
第一行包含一个整数 $n$,表示数组中有多少个数字,$1\leq n \leq 5 \cdot 10^{5}$。
第二行包含 $n$ 个整数 $a[1]$,$a[2]$,...,$a[n]$,表示数组 $a$ 的元素,其中 $|a[i]| \leq 10^{9}$。
输出格式
输出一个整数,表示将数组分成三个部分且使每部分和相等的方案数。
说明/提示
由 ChatGPT 5 翻译