CF475E Strongly Connected City 2

Imagine a city with $ n $ junctions and $ m $ streets. Junctions are numbered from $ 1 $ to $ n $ . In order to increase the traffic flow, mayor of the city has decided to make each street one-way. This means in the street between junctions $ u $ and $ v $ , the traffic moves only from $ u $ to $ v $ or only from $ v $ to $ u $ . The problem is to direct the traffic flow of streets in a way that maximizes the number of pairs $ (u,v) $ where $ 1

The first line of input contains integers $ n $ and $ m $ , (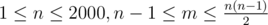), denoting the number of junctions and streets of the city. Each of the following $ m $ lines contains two integers $ u $ and $ v $ , ( $ u≠v $ ), denoting endpoints of a street in the city. Between every two junctions there will be at most one street. It is guaranteed that before mayor decision (when all streets were two-way) it was possible to reach each junction from any other junction.

Print the maximal number of pairs $ (u,v) $ such that that it is possible to reach junction $ v $ from $ u $ after directing the streets.

In the first sample, if the mayor makes first and second streets one-way towards the junction $ 1 $ and third and fourth streets in opposite direction, there would be 13 pairs of reachable junctions: $ {(1,1),(2,2),(3,3),(4,4),(5,5),(2,1),(3,1),(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)} $