CF476D Dreamoon and Sets

Dreamoon likes to play with sets, integers and . 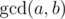 is defined as the largest positive integer that divides both $ a $ and $ b $ . Let $ S $ be a set of exactly four distinct integers greater than $ 0 $ . Define $ S $ to be of rank $ k $ if and only if for all pairs of distinct elements $ s_{i} $ , $ s_{j} $ from $ S $ , 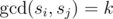. Given $ k $ and $ n $ , Dreamoon wants to make up $ n $ sets of rank $ k $ using integers from $ 1 $ to $ m $ such that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum $ m $ that makes it possible and print one possible solution.

The single line of the input contains two space separated integers $ n $ , $ k $ ( $ 1

On the first line print a single integer — the minimal possible $ m $ . On each of the next $ n $ lines print four space separated integers representing the $ i $ -th set. Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal $ m $ , print any one of them.

For the first example it's easy to see that set $ {1,2,3,4} $ isn't a valid set of rank 1 since 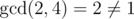.