CF482C Game with Strings

你和你的朋友玩一个游戏，游戏规则如下。 你的朋友创造出了 $n$ 个长度均为 $m$ 的不相同的字符串，然后他随机地选择其中一个。他选择这些字符串的概率是相等的，也就是说，他选择 $n$ 个字符串中的每一个的概率是 $\frac{1}{n}$。你想猜猜你的朋友选择了哪个字符串。 为了猜到你的朋友选择了哪个字符串，你可以问他问题，形式如下：字符串中第 $pos$ 个字符是什么？当这些问题的答案能够唯一确定一个字符串时，我们认为这个字符串被猜到了。在字符串被猜到后，你将停止提问。 你没有特殊的策略，所以你每次可能会等概率的问任何一个你从没猜过的位置。求猜到你的朋友选的字符串所需次数的期望。

第一行包括一个数字 $n$（$1 \le n \le 50$）。接下来 $n$ 行，每行一个字符串，表示你朋友创造出的字符串。除此之外，所有字符的长度是相同的，在 $1\sim 20$ 之间。

输出期望值，要求误差在 $10^{-9}$ 以内。

In the first sample the strings only differ in the character in the third position. So only the following situations are possible: - you guess the string in one question. The event's probability is ; - you guess the string in two questions. The event's probability is  $ · $  =  (as in this case the first question should ask about the position that is other than the third one); - you guess the string in three questions. The event's probability is  $ · $  $ · $  = ; Thus, the expected value is equal to 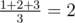 In the second sample we need at most two questions as any pair of questions uniquely identifies the string. So the expected number of questions is 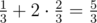. In the third sample whatever position we ask about in the first question, we immediately identify the string.