CF482D Random Function and Tree

你有一棵有 $n$ 个节点的有根树，节点编号为 $1$ 到 $n$。树的根节点是节点 $1$。对于每个 $i>1$，节点 $i$ 的直接父亲为 $p_i$。我们称节点 $i$ 是其直接父亲 $p_i$ 的子节点。 初始时，你已将所有节点涂为红色。你希望重新涂色部分节点。你通过调用 paint 函数（以树根作为参数）来涂色。以下是 paint 函数的伪代码： ``` count = 0 // 全局整数变量 rnd() { // 该函数在 paint 代码中被调用 return 0 或 1，概率相等 } paint(s) { if (count 是偶数) 则将节点 s 涂为白色 否则将节点 s 涂为黑色 count = count + 1 if rnd() = 1 则 children = [节点 s 的子节点数组，按编号升序排列] 否则 children = [节点 s 的子节点数组，按编号降序排列] 对于 children 中的每个 child { // 依次遍历 children 数组 if rnd() = 1 则 paint(child) // 递归调用 paint } } ``` 在执行完此函数后，部分节点会被涂为白色或黑色，部分节点保持红色。 你的任务是确定这棵树所有不同的可能涂色方案的数量。如果通过一次 paint(1) 调用能够有非零概率得到某种颜色分布，我们就认为该方案是可能的。如果有某对节点在两种涂色方案下颜色不同，这两种方案视为不同。由于答案可能很大，请输出其对 $1000000007$（$10^9+7$）取余后的结果。

第一行包含一个整数 $n (2 \leq n \leq 10^5)$，表示树的节点数。 第二行包含 $n-1$ 个整数 $p_2, p_3, ..., p_n (1 \leq p_i < i)$，其中 $p_i$ 表示节点 $i$ 的父节点编号。

输出一个整数，表示可能的不同涂色方案的数量，对 $1000000007$ 取余。

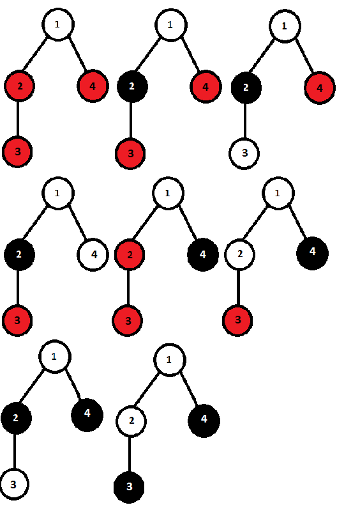
第一组样例的所有可能的涂色方案如下图所示。  由 ChatGPT 5 翻译