CF489D Unbearable Controversy of Being

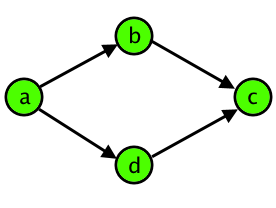
Tomash 在 Berland 的街道上闲逛时总是迷路。这也不奇怪！在他的家乡，对于任意一对交叉路口，从一个路口到另一个路口只有一条路径。而 Berland 的首都则非常不同！ Tomash 发现，即使是最简单的岔路也会让他感到困惑。因此，当他遇到四个不同的交叉路口 $a$、$b$、$c$ 和 $d$，并且从 $a$ 到 $c$ 有两条不同的路径（分别经过 $b$ 和 $d$）时，他称这群路口为“该死的菱形”。需要注意的是，$ (a,b) $、$ (b,c) $、$ (a,d) $、$ (d,c) $ 四对路口之间都应该由道路直接相连。如下图所示，这就是一个典型的“该死的菱形”：  至于这四个路口之间是否还有其他道路，这对 Tomash 来说并不会让这个菱形不那么让人讨厌，所以这里选定的四个路口仍然算作一个“该死的菱形”。 现在已知 Berland 的首都有 $n$ 个交叉路口和 $m$ 条单向道路，并且所有道路的信息都已知，请你计算城市中“该死的菱形”的数量。 对于“菱形”的计数，路口 $b$ 和 $d$ 的顺序并不重要。

输入包含多行，第一行为两个整数 $n$ 和 $m$，分别表示交叉路口的数量和道路的数量。 接下来的 $m$ 行，每行包含两个整数 $x$ 和 $y$，表示有一条从 $x$ 到 $y$ 的单向道路。

输出一个整数，即“该死的菱形”的数量。

由 ChatGPT 5 翻译