CF494D Birthday
Description
Ali is Hamed's little brother and tomorrow is his birthday. Hamed wants his brother to earn his gift so he gave him a hard programming problem and told him if he can successfully solve it, he'll get him a brand new laptop. Ali is not yet a very talented programmer like Hamed and although he usually doesn't cheat but this time is an exception. It's about a brand new laptop. So he decided to secretly seek help from you. Please solve this problem for Ali.
An $ n $ -vertex weighted rooted tree is given. Vertex number $ 1 $ is a root of the tree. We define $ d(u,v) $ as the sum of edges weights on the shortest path between vertices $ u $ and $ v $ . Specifically we define $ d(u,u)=0 $ . Also let's define $ S(v) $ for each vertex $ v $ as a set containing all vertices $ u $ such that $ d(1,u)=d(1,v)+d(v,u) $ . Function $ f(u,v) $ is then defined using the following formula:
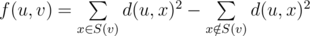The goal is to calculate $ f(u,v) $ for each of the $ q $ given pair of vertices. As the answer can be rather large it's enough to print it modulo $ 10^{9}+7 $ .
Input Format
Ali is Hamed's little brother and tomorrow is his birthday. Hamed wants his brother to earn his gift so he gave him a hard programming problem and told him if he can successfully solve it, he'll get him a brand new laptop. Ali is not yet a very talented programmer like Hamed and although he usually doesn't cheat but this time is an exception. It's about a brand new laptop. So he decided to secretly seek help from you. Please solve this problem for Ali.
An $ n $ -vertex weighted rooted tree is given. Vertex number $ 1 $ is a root of the tree. We define $ d(u,v) $ as the sum of edges weights on the shortest path between vertices $ u $ and $ v $ . Specifically we define $ d(u,u)=0 $ . Also let's define $ S(v) $ for each vertex $ v $ as a set containing all vertices $ u $ such that $ d(1,u)=d(1,v)+d(v,u) $ . Function $ f(u,v) $ is then defined using the following formula:
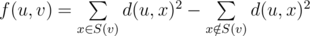The goal is to calculate $ f(u,v) $ for each of the $ q $ given pair of vertices. As the answer can be rather large it's enough to print it modulo $ 10^{9}+7 $ .
Output Format
Ali is Hamed's little brother and tomorrow is his birthday. Hamed wants his brother to earn his gift so he gave him a hard programming problem and told him if he can successfully solve it, he'll get him a brand new laptop. Ali is not yet a very talented programmer like Hamed and although he usually doesn't cheat but this time is an exception. It's about a brand new laptop. So he decided to secretly seek help from you. Please solve this problem for Ali.
An $ n $ -vertex weighted rooted tree is given. Vertex number $ 1 $ is a root of the tree. We define $ d(u,v) $ as the sum of edges weights on the shortest path between vertices $ u $ and $ v $ . Specifically we define $ d(u,u)=0 $ . Also let's define $ S(v) $ for each vertex $ v $ as a set containing all vertices $ u $ such that $ d(1,u)=d(1,v)+d(v,u) $ . Function $ f(u,v) $ is then defined using the following formula:
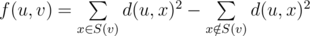The goal is to calculate $ f(u,v) $ for each of the $ q $ given pair of vertices. As the answer can be rather large it's enough to print it modulo $ 10^{9}+7 $ .