CF498E Stairs and Lines
题目描述
在一个网格上给定一个表示由 7 级台阶组成的楼梯图形。第 $i$ 层台阶的宽度为 $w_i$ 个格子。更正式地说,该图形是通过连续连接 $w_i \times i$ 大小的矩形构成的,其中每个 $w_i$ 边都在同一直线上。例如,如果所有 $w_i = 1$,那么图形如下所示(不同颜色表示不同的矩形):
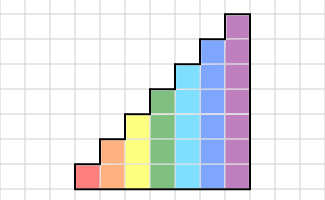
如果 $w={5,1,0,3,0,0,1}$,那么图形如下:
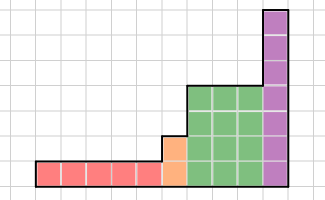
请你计算有多少种方法可以给图形内部的格子的部分边界涂色,使得每个格子都不会出现四条边都被涂色的情况。位于图形边界的方格边界视为已被涂色。不同的旋转视为不同的涂色方法。
输入格式
输入一行共 7 个数,表示 $w_1, w_2, \dots, w_7$($0 \leq w_i \leq 10^5$)。保证至少有一个 $w_i$ 不为零。
输出格式
输出一行一个整数,答案对 $10^9+7$ 取模。
说明/提示
第三个样例的所有涂色方案如下所示:
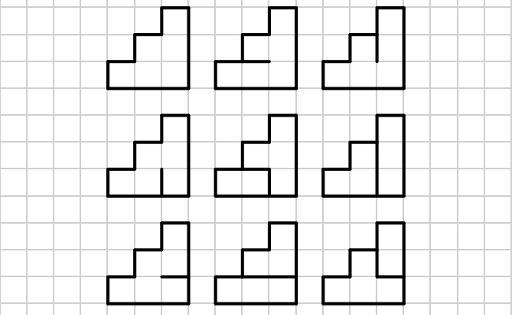
由 ChatGPT 5 翻译