CF500B New Year Permutation

User ainta has a permutation $ p_{1},p_{2},...,p_{n} $ . As the New Year is coming, he wants to make his permutation as pretty as possible. Permutation $ a_{1},a_{2},...,a_{n} $ is prettier than permutation $ b_{1},b_{2},...,b_{n} $ , if and only if there exists an integer $ k $ ( $ 1

The first line contains an integer $ n $ ( $ 1

In the first and only line, print $ n $ space-separated integers, describing the prettiest permutation that can be obtained.

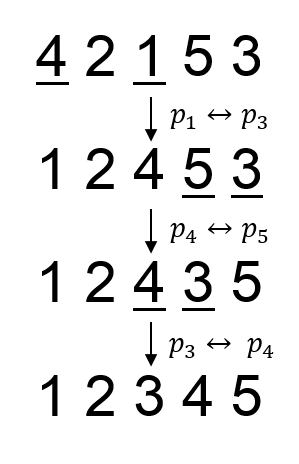
In the first sample, the swap needed to obtain the prettiest permutation is: $ (p_{1},p_{7}) $ . In the second sample, the swaps needed to obtain the prettiest permutation is $ (p_{1},p_{3}),(p_{4},p_{5}),(p_{3},p_{4}) $ . A permutation $ p $ is a sequence of integers $ p_{1},p_{2},...,p_{n} $ , consisting of $ n $ distinct positive integers, each of them doesn't exceed $ n $ . The $ i $ -th element of the permutation $ p $ is denoted as $ p_{i} $ . The size of the permutation $ p $ is denoted as $ n $ .