CF500B New Year Permutation

## 题意翻译 用户 ainta 有一个排列 $p_1,p_2,...,p_n$ 。新年到了，他希望把他的排列变得尽可能漂亮。 当且仅当存在整数 $k$（$1 \le k \le n$）使 $a_1=b_1,a_2=b_2,\ldots,a_{k-1}=b_{k-1}$ 和 $a_k

第一行包含一个整数 $n$（$1 \le n \le 300$），即排列 $p$ 的长度。 第二行包含 $n$ 个由空格分开的整数 $p_1,p_2,...,p_n$ ，保证每个不同的整数只出现一次。 接下来 $n$ 行描述矩阵 $A$ 。保证 $A_{i,j}=A_{j,i}$（$1 \le i

一行 $n$ 个空格分隔的整数，表示得到的最漂亮的排列。

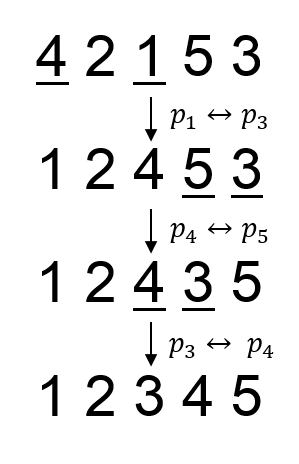
In the first sample, the swap needed to obtain the prettiest permutation is: $ (p_{1},p_{7}) $ . In the second sample, the swaps needed to obtain the prettiest permutation is $ (p_{1},p_{3}),(p_{4},p_{5}),(p_{3},p_{4}) $ . A permutation $ p $ is a sequence of integers $ p_{1},p_{2},...,p_{n} $ , consisting of $ n $ distinct positive integers, each of them doesn't exceed $ n $ . The $ i $ -th element of the permutation $ p $ is denoted as $ p_{i} $ . The size of the permutation $ p $ is denoted as $ n $ .