CF500E New Year Domino

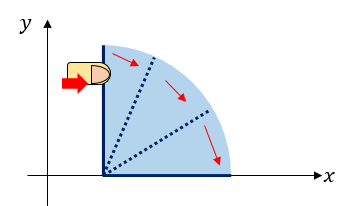为庆祝新年，许多人会发布多米诺骨牌倒塌的视频；这里有一个相关的列表：https://www.youtube.com/results?search\_query=New+Years+Dominos 用户 ainta 生活在二维世界，他也打算发布这样一个视频。 在二维平面直角坐标系上有 $n$ 个多米诺骨牌。第 $i$ 个多米诺骨牌（$1 \leq i \leq n$）可以表示为一条与 $y$ 轴平行、长度为 $l_i$ 的线段，其下端点在 $x$ 轴上。我们用 $p_i$ 表示第 $i$ 个骨牌的 $x$ 坐标。多米诺骨牌依次摆放，满足 $p_1 < p_2 < \cdots < p_{n-1} < p_n$。 用户 ainta 想拍一段多米诺骨牌倒塌的视频。为了让骨牌倒下，他可以将某一块骨牌向右推倒。然后，这块骨牌会绕下端点画出半圆轨迹，直到整条线段与 $x$ 轴重合。 另外，如果第 $s$ 块骨牌在倒下时碰触到了第 $t$ 块骨牌，则第 $t$ 块骨牌也会朝右倒下，并以同样的方式继续倒塌。仅当 $s$ 与 $t$ 表示的两条线段相交时，$s$ 才能碰到 $t$。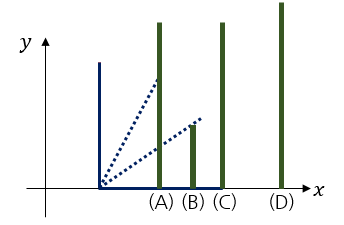 如上图所示。如果他最先推倒最左边的骨牌，它倒下时会依次碰到（A）、（B）和（C）三块骨牌，因此它们也会继续往右倒。然而，骨牌（D）不会直接被最左边的骨牌带倒，而是在被骨牌（C）首次碰到时才会倒下。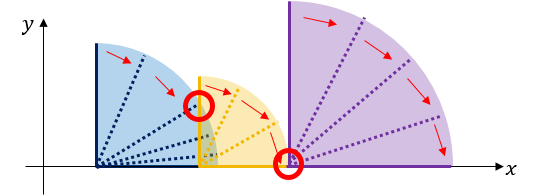 上图是一个多米诺骨牌倒塌的示例，每个红圈表示两块骨牌的接触点。 用户 ainta 有 $q$ 个发布计划，第 $j$ 个计划开始时先推倒第 $x_j$ 块骨牌，直到第 $y_j$ 块骨牌倒下为止。但有时无法直接实现这样的计划，因此需要适当延长一些骨牌的长度。将任意一块骨牌的长度增加 $1$ 需要花费 $1$ 美元。对于每个计划，用户想知道实现该计划所需的最小花费。各个计划之间相互独立，即便某个计划中骨牌的长度被延长，其他计划中仍然按原长度计算。除了第 $x_j$ 块骨牌和第 $y_j$ 块骨牌，其余骨牌倒不倒下无所谓，但推倒操作必须从第 $x_j$ 块骨牌开始。

第一行包含一个整数 $n$（$2 \leq n \leq 2 \times 10^5$），表示骨牌的数量。 接下来 $n$ 行，每行包含两个用空格分隔的整数 $p_i, l_i$（$1 \leq p_i, l_i \leq 10^9$），分别代表第 $i$ 个骨牌的 $x$ 坐标和长度。保证 $p_1 < p_2 < \cdots < p_n$。 接下来一行包含一个整数 $q$（$1 \leq q \leq 2 \times 10^5$），表示计划的数量。 接下来的 $q$ 行，每行包含两个用空格分隔的整数 $x_j, y_j$（$1 \leq x_j < y_j \leq n$），表示第 $j$ 个计划，即从第 $x_j$ 块骨牌推倒，直到第 $y_j$ 块骨牌倒下。

对于每个计划，输出实现该计划所需的最小花费，每行一个整数。如果不需要任何花费，则输出 $0$。

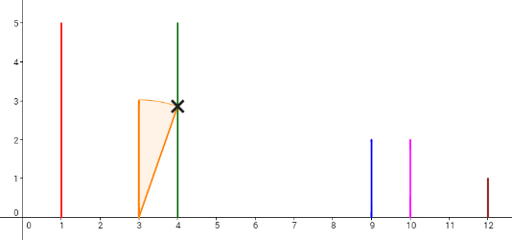
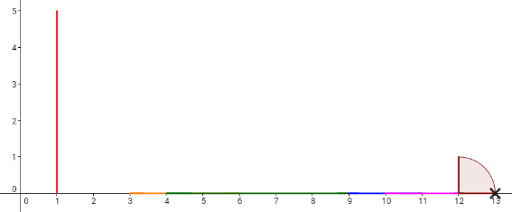
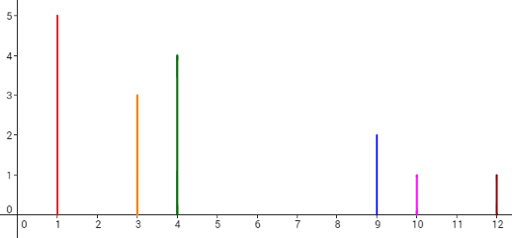例如，骨牌的摆放如图所示。 来看第 4 个计划。要从第 2 块骨牌推倒第 6 块骨牌，必须将第 3 块骨牌（其 $x$ 坐标为 $4$）加长 $1$，第 5 块骨牌（其 $x$ 坐标为 $9$）也需加长 $1$（另一种选择是加长第 4 块骨牌 $1$ 而不加第 5 块）。然后，多米诺骨牌的倒塌过程如下图所示，每个叉号表示两块骨牌接触：      由 ChatGPT 5 翻译