CF507C Guess Your Way Out!

Amr 买了一款新电子游戏“Guess Your Way Out!”。游戏的目标是在一个高度为 $h$ 的完美二叉树状迷宫中找到出口。玩家最初站在树的根节点，出口位于某个叶子节点。 我们将所有的叶子节点从左到右编号为 $1$ 到 $2^h$。出口位于编号为 $n$ 的节点上，其中 $1 \leq n \leq 2^h$，玩家并不知道出口的位置，因此只能靠猜测来逃离！ Amr 遵循一个简单的算法来选择路径。我们以无限长的指令串“LRLRLRLRL...”为例（由交替的 'L' 和 'R' 字符组成）。Amr 依次执行字符串中的字符，遵循以下规则： - 字符 'L' 表示“前往当前节点的左儿子”； - 字符 'R' 表示“前往当前节点的右儿子”； - 如果目标节点已经被访问过，Amr 会跳过当前指令，否则他就移动到目标节点； - 如果连续跳过两条指令，Amr 会在执行下一条指令前返回当前节点的父节点； - 如果到达的是不是出口的叶子节点，Amr 回到当前节点的父节点； - 如果到达出口，则游戏结束。 现在 Amr 很好奇，如果他按照这种算法行动，在到达出口前最多会经过多少个节点？

输入包含两个整数 $h, n$，满足 $1 \leq h \leq 50$，$1 \leq n \leq 2^{h}$。

输出一个整数，表示按照上述算法，Amr 在到达出口前会访问多少个节点（不包含出口节点本身）。

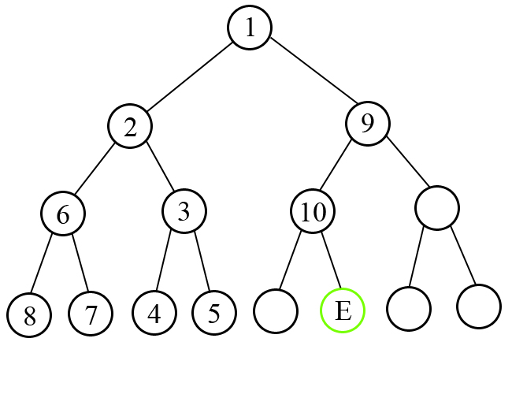
高度为 $h$ 的完美二叉树由 $h+1$ 层组成。第 $0$ 层包含一个根节点，第 $h$ 层包含 $2^h$ 个节点，这些节点称为叶子节点。除叶子节点外的每个节点都有且仅有两个儿子，分别为左儿子和右儿子。 下图展示了样例测试 $3$ 的情况。节点标号表示访问顺序。  由 ChatGPT 5 翻译