CF50D Bombing

The commanding officers decided to drop a nuclear bomb on the enemy's forces. You are ordered to determine the power of the warhead that needs to be used. The enemy has $ N $ strategically important objects. Their positions are known due to the intelligence service. The aim of the strike is to deactivate at least $ K $ important objects of the enemy. The bombing impact point is already determined and has coordinates of $ [X_{0};\ Y_{0}] $ . The nuclear warhead is marked by the estimated impact radius $ R>=0 $ . All the buildings that are located closer than $ R $ to the bombing epicentre will be destroyed. All the buildings that are located further than $ R $ from the epicentre, can also be deactivated with some degree of probability. Let's assume that $ D $ is the distance between a building and the epicentre. This building's deactivation probability $ P(D,R) $ is calculated according to the following formula: 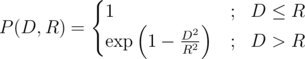 We should regard 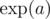 as $ e^{a} $ , where $ e≈2.7182818284590452353602874713527 $ If the estimated impact radius of the warhead is equal to zero, then all the buildings located in the impact point will be completely demolished and all the rest of important objects will not be damaged. The commanding officers want the probability of failing the task to be no more than $ ε $ . Nuclear warheads are too expensive a luxury, that's why you have to minimise the estimated impact radius of the warhead.

The first line contains an integer $ N $ which represents the number of the enemy's objects ( $ 1

Print the sought estimated impact radius of the warhead. The absolute or relative measure of the inaccuracy of your answer should not exceed $ 10^{-6} $ .