CF50D Bombing
题目描述
指挥官们决定对敌军部队投放一枚核弹。你被命令确定需要使用的弹头威力。
敌方有 $N$ 个战略重要目标,其位置已由情报部门获知。本次打击的目标是至少摧毁敌方 $K$ 个重要目标。轰炸的爆心点已确定,坐标为 $[X_{0}, Y_{0}]$。
核弹头的杀伤力由其预计影响半径 $R \geq 0$ 表示。所有距离爆心点小于 $R$ 的建筑物将被摧毁。所有距离爆心点大于等于 $R$ 的建筑物,也有一定概率被摧毁。设某建筑与爆心点距离为 $D$,该建筑被摧毁的概率 $P(D,R)$ 按照下述公式计算:
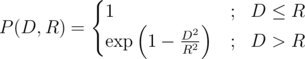
其中 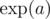 表示 $e^a$,其中 $e \approx 2.7182818284590452353602874713527$。
如果弹头的预计影响半径 $R$ 等于零,则所有位于爆心点的目标将被完全摧毁,其余重要目标不会受到损伤。
指挥官希望任务失败的概率不超过 $ε$。核弹头极其昂贵,因此你需要最小化弹头的预计影响半径。
输入格式
第一行包含一个整数 $N$,表示敌方目标数量($1 \leq N \leq 100$)。
第二行包含两个整数:$K$ 表示至少需摧毁的目标数,$ε$ 表示可允许的最大任务失败概率,以千分数(per mils)给出($1 \leq K \leq N$,$1 \leq ε \leq 999$)。
第三行包含 $X_{0}$ 和 $Y_{0}$,即爆心点坐标。
接下来的 $N$ 行,每行包含两个数 $X_{i}, Y_{i}$,表示每个重要目标的坐标。所有坐标均为整数,取值的绝对值不超过 $1000$。
注意,一个点上可能存在多个目标。
输出格式
输出所需的弹头预计影响半径。答案的绝对或相对误差不超过 $10^{-6}$。
说明/提示
由 ChatGPT 5 翻译