CF50E Square Equation Roots
题目描述
小学生 Petya 学习二次方程。学校课程中出现的方程通常很简单:
$$
x^{2} + 2bx + c = 0
$$
其中 $b$、$c$ 是自然数。Petya 发现,有些方程有两个实数根,有些只有一个根,还有一些没有实数根。此外,不同的二次方程可能会有公共的根。
现在 Petya 想知道,对于所有满足 $1 \leq b \leq n$ 且 $1 \leq c \leq m$ 的 $b$ 和 $c$,上述类型的所有方程一共会有多少个不同的实数根。请你帮助 Petya 找出这个数字。
输入格式
输入一行包含两个整数 $n$ 和 $m$,分别表示 $b$ 和 $c$ 的上界。$(1 \leq n, m \leq 5000000)$。
输出格式
输出一个整数,表示这些方程所有不同实数根的个数。
说明/提示
在第二个样例中,有以下方程:
$b=1$,$c=1$:$x^2+2x+1=0$;根为 $x=-1$。
$b=1$,$c=2$:$x^2+2x+2=0$;无实根。
总体来说只有一个根。
在第三个样例中,分析如下:
$b=1$,$c=1$:$x^2+2x+1=0$;根为 $x=-1$。
$b=1$,$c=2$:$x^2+2x+2=0$;无实根。
$b=1$,$c=3$:$x^2+2x+3=0$;无实根。
$b=2$,$c=1$:$x^2+4x+1=0$;根为 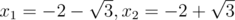
$b=2$,$c=2$:$x^2+4x+2=0$;根为 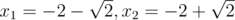
$b=2$,$c=3$:$x^2+4x+3=0$;根为 $x_1=-3, x_2=-1$。
$b=3$,$c=1$:$x^2+6x+1=0$;根为 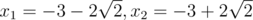
$b=3$,$c=2$:$x^2+6x+2=0$;根为 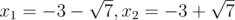
$b=3$,$c=3$:$x^2+6x+3=0$;根为 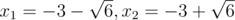
总共有 $13$ 个根,因为 $-1$ 重复出现了一次,所以不同的根有 $12$ 个。
由 ChatGPT 5 翻译