CF513G3 Inversions problem

You are given a permutation of $ n $ numbers $ p_{1},p_{2},...,p_{n} $ . We perform $ k $ operations of the following type: choose uniformly at random two indices $ l $ and $ r $ ( $ l

The first line of input contains two integers $ n $ and $ k $ ( $ 1

Output the answer with absolute or relative error no more than $ 1e-9 $ .

Consider the first sample test. We will randomly pick an interval of the permutation $ (1,2,3) $ (which has no inversions) and reverse the order of its elements. With probability , the interval will consist of a single element and the permutation will not be altered. With probability  we will inverse the first two elements' order and obtain the permutation $ (2,1,3) $ which has one inversion. With the same probability we might pick the interval consisting of the last two elements which will lead to the permutation $ (1,3,2) $ with one inversion. Finally, with probability  the randomly picked interval will contain all elements, leading to the permutation $ (3,2,1) $ with 3 inversions. Hence, the expected number of inversions is equal to 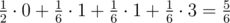.