CF516D Drazil and Morning Exercise

Drazil 和 Varda 是一对蚯蚓夫妻。他们想要找一个合适的地方抚养孩子。他们发现了一块有天然洞穴的好土壤。这个洞中有许多房间，部分房间之间通过小隧道连接，这样蚯蚓就能在它们之间移动。 我们可以把房间和小隧道看作图中的点和边。这个图是一棵树。换句话说，任意两点之间都有且只有一条唯一的路径。 每一个在图中是叶子的房间通过一条竖直的隧道与地面相连。这里的“叶子”指的是在图中只有一条出边的点。 每个房间都只能容纳一只蚯蚓居住。蚯蚓不能住在隧道里。 Drazil 和 Varda 有个计划要教育他们的孩子。他们希望所有的孩子起床后立刻做晨操！ 早上来临时，所有的蚯蚓孩子会同时起床，然后每个人都会选择距离地面最远的路径下去，与其他小伙伴汇合（这些小孩都很懒，所以他们都想尽量晚点开始运动）。 Drazil 和 Varda 希望，第一个到达地面的孩子与最后一个到达地面的孩子之间的到达时间差不超过 $l$（否则孩子们会分散在地面上，很难一起做运动）。 此外，被孩子们占据的房间应当形成一个连通块。换句话说，对于任意两间有孩子居住的房间，所有在它们之间路径上的房间也必须有孩子住。 问：在满足上述所有条件的前提下，Drazil 和 Varda 最多可以有多少个孩子？对于不同的 $l$，Drazil 和 Varda都想知道答案。 （Drazil 和 Varda 不和孩子们住在洞穴里）

第一行包含一个整数 $n$，表示洞中共有多少间房间（$2 \le n \le 10^{5}$）。 接下来有 $n-1$ 行，每行包含三个整数 $x, y, v$（$1 \le x,y \le n$，$1 \le v \le 10^{6}$），表示房间 $x$ 与房间 $y$ 之间有一条需要花费 $v$ 单位时间通过的小隧道。 假设每个叶子房间通向地面的竖直隧道所需的时间都是相同的。 下一行包含一个整数 $q$（$1 \le q \le 50$），表示需要处理的不同 $l$ 的数量。 最后一行包含 $q$ 个数字，每个数字表示一个 $l$ 的值（$1 \le l \le 10^{11}$）。

输出 $q$ 行。每行一个整数，表示对应 $l$ 情况下的答案。

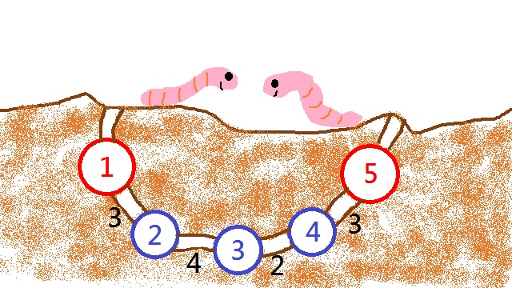
对于第一个样例，洞穴的结构如下图所示。房间 $1$ 和 $5$ 是叶子，所以它们都通过一条竖直隧道与地面相连。从房间 $1$ 到 $5$ 各自距离地面的最远路径长度分别为 $12, 9, 7, 9, 12$。 如果 $l = 1$，我们只能选择任意一间房间。 如果 $l = 2\sim 4$，我们可以选择房间 $2, 3, 4$ 作为答案。 如果 $l = 5$，我们可以选择所有房间。  由 ChatGPT 5 翻译