CF51F Caterpillar

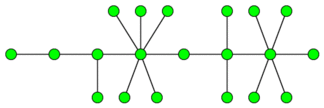
若一个无向连通无环图上存在一条路径 $p$ 使得任意一个节点距离 $p$ 的距离至多为 $1$，则它被称为一个毛毛虫。毛毛虫可以包含自环（一条从一个顶点连向自己的边），但是不可以包含重边。 这张图片是一个毛毛虫的例子：  给定一张无向图 $G$。你可以做一些合并操作，每次操作将两个顶点合并成一个顶点。每次选择任意两个顶点 $a,b$（$a\ne b$）, 这些顶点以及它们的边（端点是 $a,b$ 中至少一个点的边）将被删除，而后加入顶点 $w$，以及对于每条边 $(x,a),(x,b)$ 都会加入新边 $(x,w)$。如果有一条边 $(a,b)$，它会被转换成自环 $(w,w)$。得到的图（操作结束后）可能会有重边。我们注意到这个操作减少了 $1$ 个顶点，却没有改变边的数量。 合并操作可以简单的描述为将图中两个顶点合并为图中的一个顶点并继承原来所有的边。 你可以连续使用合并操作，将给定的图转变成一个毛毛虫。计算这张图转变成一个毛毛虫的最少操作次数。

第一行包含两个正整数 $n,m$（$1\le n\le2000,1\le m\le10^5$），$n$ 代表图中顶点的数量，$m$ 代表边的数量。接下来 $m$ 行描述边的信息，每行一条。每行一对整数 $a_i,b_i$（$1\le a_i,b_i\le n,a_i\ne b_i$），表示一条边。顶点从 $1$ 到 $n$ 编号，保证任意两点间不会有多条边，图不一定连通。

输出操作次数的最小值。