CF523B Mean Requests

In this problem you will have to deal with a real algorithm that is used in the VK social network. As in any other company that creates high-loaded websites, the VK developers have to deal with request statistics regularly. An important indicator reflecting the load of the site is the mean number of requests for a certain period of time of $ T $ seconds (for example, $ T=60 seconds=1 min $ and $ T=86400 seconds=1 day $ ). For example, if this value drops dramatically, that shows that the site has access problem. If this value grows, that may be a reason to analyze the cause for the growth and add more servers to the website if it is really needed. However, even such a natural problem as counting the mean number of queries for some period of time can be a challenge when you process the amount of data of a huge social network. That's why the developers have to use original techniques to solve problems approximately, but more effectively at the same time. Let's consider the following formal model. We have a service that works for $ n $ seconds. We know the number of queries to this resource $ a_{t} $ at each moment of time $ t $ ( $ 1

The first line contains integer $ n $ ( $ 1

Print $ m $ lines. The $ j $ -th line must contain three numbers $ real $ , $ approx $ and $ error $ , where: - 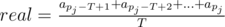 is the real mean number of queries for the last $ T $ seconds; - $ approx $ is calculated by the given algorithm and equals $ mean $ at the moment of time $ t=p_{j} $ (that is, after implementing the $ p_{j} $ -th iteration of the cycle); - 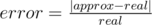 is the relative error of the approximate algorithm. The numbers you printed will be compared to the correct numbers with the relative or absolute error $ 10^{-4} $ . It is recommended to print the numbers with at least five digits after the decimal point.