CF526B Om Nom and Dark Park

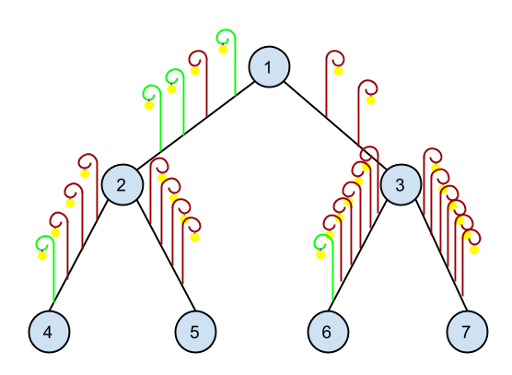
Om Nom 是游戏“Cut the Rope”的主角。他是一个聪明的小怪兽，喜欢拜访住在公园另一头的朋友们。然而，昏暗老旧的公园即使对无所畏惧的 Om Nom 也有些吓人，于是他请求你帮助他。 公园由 $2^{n+1}-1$ 个广场组成，这些广场通过道路相连，形成一个深度为 $n$ 的满二叉树结构。更正式地说，公园的入口位于广场 $1$。公园的出口位于广场 $2^{n},2^{n}+1,...,2^{n+1}-1$，这些出口直通 Om Nom 的朋友们家。从每个广场 $i$（$2 \leq i < 2^{n+1}$）都有一条道路通向广场 $\left\lfloor \frac{i}{2} \right\rfloor$。因此，从入口出发到任一出口，需要恰好经过 $n$ 条道路。 为了在晚上照亮道路，园丁在每条道路上安装了路灯。连接广场 $i$ 和 $\left\lfloor \frac{i}{2} \right\rfloor$ 的道路上有 $a_i$ 盏路灯。Om Nom 喜欢数去朋友家的路上看到的路灯数量。但他害怕居住在公园里的蜘蛛，所以他不喜欢走那些照明不足的路。他希望从入口到任一朋友家的路径上，路灯总数都一样，这样才能让他感到安全。 他请求你帮助安装更多的路灯。请你计算，为了让从入口到所有出口的路径上路灯总数都相同，最少还需要在公园的道路上再安装多少盏路灯。你可以在每条道路上添加任意数量的路灯。

第一行包含一个整数 $n$（$1 \leq n \leq 10$），表示从入口到任一出口的路径上有 $n$ 条道路。 第二行包含 $2^{n+1}-2$ 个整数 $a_2, a_3, ... , a_{2^{n+1}-1}$，表示公园里每条道路最初安装的路灯数量。这里，$a_i$ 表示连接广场 $i$ 和 $\left\lfloor \frac{i}{2} \right\rfloor$ 的道路上的路灯数。所有 $a_i$ 都是不超过 $100$ 的正整数。

输出一个整数，表示至少还需要在公园的道路上安装多少盏路灯，才能让 Om Nom 感到安全。

下图为样例测试的情形。绿色部分表示新加的路灯。  由 ChatGPT 5 翻译