CF528E Triangles 3000

You are given a set $ L={l_{1},l_{2},...,l_{n}} $ of $ n $ pairwise non-parallel lines on the Euclidean plane. The $ i $ -th line is given by an equation in the form of $ a_{i}x+b_{i}y=c_{i} $ . $ L $ doesn't contain three lines coming through the same point. A subset of three distinct lines is chosen equiprobably. Determine the expected value of the area of the triangle formed by the three lines.

The first line of the input contains integer $ n $ ( $ 3

Print a single real number equal to the sought expected value. Your answer will be checked with the absolute or relative error $ 10^{-4} $ .

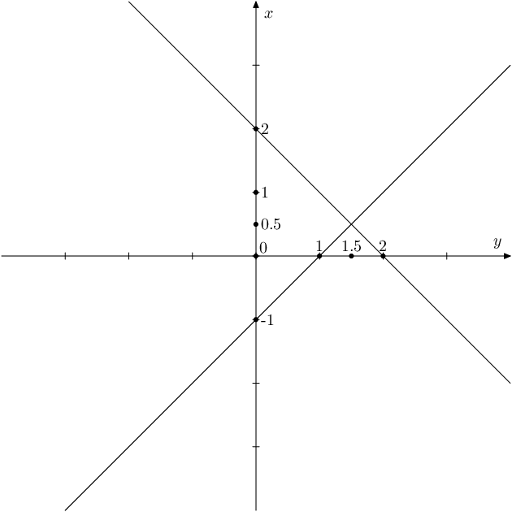
A sample from the statement is shown below. There are four triangles on the plane, their areas are $ 0.25,0.5,2,2.25 $ .