CF528E Triangles 3000
题目描述
给定平面上的$n$个不平行的直线。第$i$条直线以方程$a_ix+b_iy=c_i$的方式给定。没有三线交于一点的情况。
求出任意三条直线形成的三角形的面积之和。
输入格式
第一行一个整数,$n$。
接下来$n$行,每行三个整数,$a_i$,$b_i$,$c_i$。
数据满足$n \leq 3,000$, $-100\leq a_i,b_i\leq 100$, ${a_i}^2+{b_i}^2\geq 0$, $-1000 \leq c_i \leq 10000$
数据保证没有两条直线平行,任意两条直线的夹角$\geq 10^{-4}$
$I$是直线的交点的集合,即$I=\left\{l_{i} \cap l_{j} | i
输出格式
输出答案。允许误差$10^{-4}$。
## 样例解释
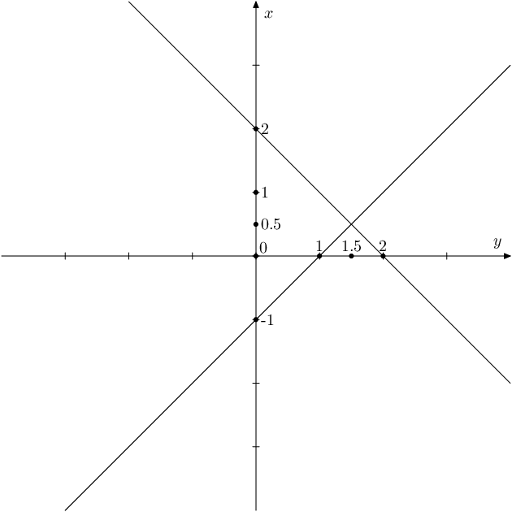
共4个三角形,面积为$0.25$, $0.5$, $2$, $2.25$
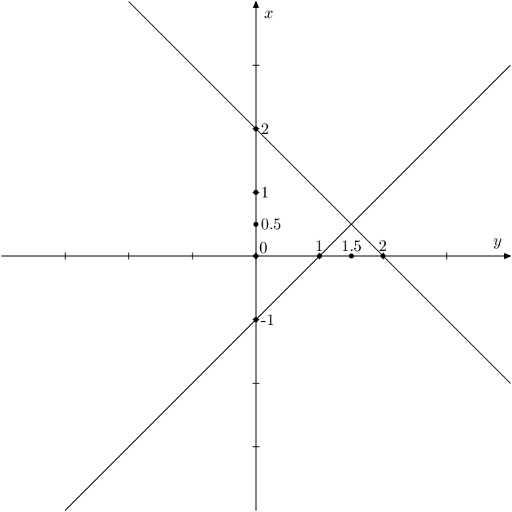
说明/提示
A sample from the statement is shown below. There are four triangles on the plane, their areas are $ 0.25,0.5,2,2.25 $ .