CF533A Berland Miners

伯兰德最大的金矿由 $n$ 个洞穴构成，这些洞穴通过 $n-1$ 条通道相连。矿洞的入口通向第 $1$ 号洞穴，可以通过通道从入口到达矿洞的任意一个洞穴。 该矿由 InMine Inc. 公司开发，雇佣了 $k$ 名矿工。公司每天将矿工分配到各个洞穴，每个洞穴最多只能有一名矿工工作。 每个洞穴的顶高为 $h_i$ 米，每个矿工的身高为 $s_j$ 米。如果矿工的身高不超过所在洞穴的顶高，则他可以舒适地站立，否则就不得不弯腰，这会让他感到不满。 由于在伯兰德矿工罢工屡见不鲜，InMine Inc. 非常重视矿工的工作条件。公司要求，无论矿工从矿洞入口到达工作的洞穴过程中，途经的所有洞穴的顶高都不能低于他的身高（特别是他工作的那个洞穴），否则他就必须弯腰。 为实现这一目标，你可以选择恰好一个洞穴，将其顶高提升若干米。然而扩建洞穴十分昂贵且复杂。因此，InMine Inc. 请你计算：要使所有矿工都能被分配到洞穴且在工作条件下感到满意，至少需要将某个洞穴的顶高提升多少米；或者判断仅通过提升一个洞穴的顶高，能否实现上述条件。

第一行包含整数 $n$（$1 \le n \le 5 \cdot 10^5$），表示矿洞中的洞穴数。 第二行为 $n$ 个正整数 $h_1, h_2, ..., h_n$（$1 \le h_i \le 10^9$），表示第 $i$ 个洞穴的顶高。 接下来 $n-1$ 行，每行包含两个整数 $a_i, b_i$（$1 \le a_i, b_i \le n$，$a_i \neq b_i$），表示第 $a_i$ 号洞穴与第 $b_i$ 号洞穴之间有一条通道。 接着一行包含整数 $k$（$1 \le k \le n$），表示矿工人数。 最后一行包含 $k$ 个整数 $s_1, s_2, ..., s_k$（$1 \le s_j \le 10^9$），表示第 $j$ 个矿工的身高。

输出一个整数，表示为满足所有矿工的工作条件，至少需要将某个洞穴的顶高提升多少米。如果无论如何都无法通过提升恰好一个洞穴实现目标，输出 $-1$。如果无需提升即可满足所有矿工需求，输出 $0$。

在第一个样例中，应将第一个洞穴的顶高从 $5$ 提升到 $11$。之后可以如下分配矿工（前为矿工编号，后为洞穴编号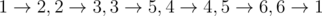）：。 在第二个样例中，不需要做任何操作。可以如下分配矿工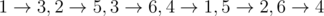：。 第三个样例中是无解的。 由 ChatGPT 5 翻译