CF534E Berland Local Positioning System

在伯兰德的首都，有一辆公交车在主街上行驶。该街道从中心广场开始，看起来就像一条非常长的线段。街道上设有 $ n $ 个公交站，第 $ i $ 个车站距离中心广场的距离为 $ a_{i} $，所有车站之间的距离各不相同。车站按照距离从小到大的顺序编号，即对于每个 $ i $ 从 1 到 $ n-1 $ 有 $ a_{i} < a_{i+1} $。公交车从第一个车站出发，依次经过第 2、3 等车站，一直行驶到第 $ n $ 个车站，然后调头返回第一个车站，沿途按相反顺序经过所有中间车站。之后，它又朝着第 $ n $ 个车站行驶。公交车全天不停地在这条路线上往返。 公交车装配了伯兰德当地的定位系统。当公交车经过某个车站时，系统会记录下该车站的编号。 这个系统的一个重要功能是可以回答关于公交车在某些路径段上行驶距离的询问。系统模块会接收包含路径某段区间内车站集合的信息，每个车站编号出现的次数等同于公交车反复经过的次数。这个模块返回路径区间的行程距离（如果无法唯一确定行程距离，则返回 -1）。复杂性在于，请求中的车站编号并非以访问顺序排列，而是按非递减顺序排列。 例如，如果总共有 6 个车站，公交车某段路径从第 5 号站开始，结束于第 3 号站，并按以下顺序经过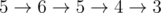：，则这个路径的请求形式为：$ 3, 4, 5, 5, 6 $。如果在从第 5 号站到第 3 号站途中，公交车还经过了第 1 号站（即考虑它到达第 3 号站的第二次路程），请求形式则变为：$ 1, 2, 2, 3, 3, 4, 5, 5, 6 $。 您需要编写程序实现此功能。

- 第一行输入一个整数 $ n $（$ 2 \leq n \leq 2 \cdot 10^{5} $），表示车站的数量。 - 第二行输入 $ n $ 个整数（$ 1 \leq a_{i} \leq 10^{9} $），表示每个车站到中心广场的距离。这些数字按递增顺序排列。 - 第三行输入一个整数 $ m $（$ 1 \leq m \leq 4 \cdot 10^{5} $），表示公交车在某段路径上经过的车站总数。 - 第四行输入 $ m $ 个整数（$ 1 \leq b_{i} \leq n $），表示以排序顺序列出的公交车经过的车站的编号。每个车站编号出现的次数等于公交车反复经过它的次数。 保证每一个查询对应某段实际路径。

输出公交车行驶的路程距离。如果无法唯一判定该距离，输出 -1。

第一个测试用例展示了题目中的第一个例子。 第二个测试用例展示了题目中的第二个例子。 在第三个样例中，存在两条可能的路径且长度不同，因此所求的路径长度无法确定。 在第四个样例中，尽管存在两条不同的路径对应于请求，但它们的长度相同，因此路径长度是唯一确定的。 **本翻译由 AI 自动生成**