CF536E Tavas on the Path

Tavas lives in Tavaspolis. Tavaspolis has $ n $ cities numbered from $ 1 $ to $ n $ connected by $ n-1 $ bidirectional roads. There exists a path between any two cities. Also each road has a length. Tavas' favorite strings are binary strings (they contain only 0 and 1). For any binary string like $ s=s_{1}s_{2}...\ s_{k} $ , $ T(s) $ is its $ Goodness $ . $ T(s) $ can be calculated as follows: Consider there are exactly $ m $ blocks of $ 1 $ s in this string (a block of $ 1 $ s in $ s $ is a maximal consecutive substring of $ s $ that only contains $ 1 $ ) with lengths $ x_{1},x_{2},...,x_{m} $ . Define 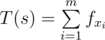 where $ f $ is a given sequence (if $ m=0 $ , then $ T(s)=0 $ ). Tavas loves queries. He asks you to answer $ q $ queries. In each query he gives you numbers $ v,u,l $ and you should print following number: Consider the roads on the path from city $ v $ to city $ u $ : $ e_{1},e_{2},...,e_{x} $ . Build the binary string $ b $ of length $ x $ such that: $ b_{i}=1 $ if and only if $ l

The first line of input contains integers $ n $ and $ q $ ( $ 2

Print the answer of each query in a single line.