CF536E Tavas on the Path

Tavas 住在 Tavaspolis。Tavaspolis 有 $ n $ 个城市，编号从 $ 1 $ 到 $ n $，通过 $ n-1 $ 条双向道路相连。任意两个城市之间都存在一条路径。每条道路都有一个长度。 Tavas 最喜欢的字符串是二进制字符串（仅包含 $0$ 和 $1$）。对于任意一个二进制字符串 $ s=s_{1}s_{2}...\ s_{k} $，定义 $ T(s) $ 为其 $ Goodness $。$ T(s) $ 的计算方式如下： 设字符串中恰好有 $ m $ 个连续 $1$ 的区块（即 $1$ 的区块指仅包含 $1$ 的极大连续子串），每个区块的长度为 $ x_{1},x_{2},...,x_{m} $。 定义 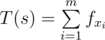 其中 $ f $ 是给定的序列（若 $ m=0 $，则 $ T(s)=0 $）。 Tavas 喜欢提问。现在他会提出 $ q $ 个询问。每个询问给出 $ v,u,l $ 让你输出如下的值： 令城市 $ v $ 到城市 $ u $ 之间路径上的道路编号为 $ e_{1},e_{2},...,e_{x} $。 构造一个长度为 $ x $ 的二进制字符串 $ b $，使得：若 $ l \leq w(e_{i}) $，则 $ b_{i}=1 $，否则 $ b_{i}=0 $，其中 $ w(e) $ 表示道路 $ e $ 的长度。 对于每个询问，请输出 $ T(b) $。

输入的第一行包含整数 $ n $ 和 $ q $（$ 2 \leq n \leq 10^{5} $，$ 1 \leq q \leq 10^{5} $）。 第二行包含 $ n-1 $ 个用空格分隔的整数 $ f_{1},f_{2},...,f_{n-1} $（$ |f_{i}| \leq 1000 $）。 接下来 $ n-1 $ 行，每行包含三个整数 $ v,u $ 和 $ w $，表示城市 $ v $ 和 $ u $ 之间有一条长度为 $ w $ 的道路（$ 1 \leq v,u \leq n $，$ 1 \leq w \leq 10^{9} $）。 接下来 $ q $ 行，每行包含三个整数 $ v,u,l $（$ 1 \leq v,u \leq n $，$ v \neq u $，$ 1 \leq l \leq 10^{9} $）。

对于每个询问输出一行，每行一个答案。

由 ChatGPT 5 翻译