CF540E Infinite Inversions

有一个按升序排列的无限正整数序列 $p = \{1, 2, 3, \dots\}$。我们对该序列进行了 $n$ 次交换操作。一次 $swap(a, b)$ 操作表示交换序列中第 $a$ 个和第 $b$ 个位置上的元素。你的任务是计算最终序列中逆序对的数量，即满足 $i < j$ 且 $p_i > p_j$ 的索引对 $(i, j)$ 的个数。

第一行包含一个整数 $n$（$1 \leq n \leq 10^{5}$），表示执行了多少次交换操作。 接下来的 $n$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq 10^{9}$，$a_i \ne b_i$），表示一次交换操作的两个位置参数。

输出一个整数，表示最终序列中的逆序对数量。

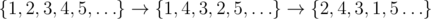
在第一个样例中，序列的变化如下：  其中，共有 4 个逆序对，分别是 $(1,4)$、$(2,3)$、$(2,4)$ 和 $(3,4)$。 由 ChatGPT 5 翻译