CF542D Superhero's Job

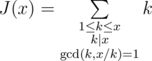成为超级英雄并不容易，而要抗拒那些擅长数学的超级反派则更加艰难。假设你只是哥谭市一名普通的蝙蝠侠。你的敌人小丑在市政府大楼中安置了炸弹，你只有几分钟的时间来解除爆炸装置。要想完成解除，你需要在炸弹控制面板上输入终止密码。 不过，这个疯狂家伙给了你一点线索。今天早晨，市长在自己的枕头下发现了一张扑克牌。牌上写着一行字： 炸弹上有一张便条，写着“ $J(x)=A$ ”，其中 $A$ 是一个正整数。你怀疑终止密码就是某个满足 $J(x)=A$ 的整数 $x$。现在，为了判断你是否应当解除炸弹还是临阵脱逃，你要计算有多少个不同的正整数 $x$ 满足该等式。

输入的唯一一行包含一个整数 $A$，其中 $1\le A\le 10^{12}$。

输出满足方程 $J(x)=A$ 的正整数 $x$ 的个数。

记 $x\mid n$ 表示数 $n$ 能整除数 $x$。 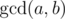 定义为同时整除 $a$ 和 $b$ 的最大正整数。 在第一个样例测试中，唯一合适的 $x$ 为 $2$。此时 $J(2)=1+2$。 在第二个样例测试中，符合条件的 $x$ 有： - $x=14$，$J(14)=1+2+7+14=24$； - $x=15$，$J(15)=1+3+5+15=24$； - $x=23$，$J(23)=1+23=24$。 由 ChatGPT 5 翻译