CF542E Playing on Graph

Vova 和 Marina 喜欢互相出谜题。今天，Marina 给 Vova 出了如下任务。 Vova 有一个包含 $n$ 个点 $m$ 条边的无向图，图中没有自环和重边。我们定义“收缩”操作为：选择两个未直接相连的顶点 $a$ 和 $b$，用一个新顶点 $x$ 代替它们，并且将原本与 $a$ 或 $b$ 相连的所有点都连一条边到 $x$；如果一个点既和 $a$ 相连又和 $b$ 相连，则只连接一条边到 $x$。经过一次收缩操作，图仍然是无向图且无自环和重边，点数减少为 $n-1$。 Vova 可以任意次数地进行收缩操作，目标是将原图变为一条长度尽可能长的链。长度为 $k$ 的链（$k \ge 0$）指的是一种连通图，顶点可以编号为 $1$ 到 $k+1$，图中只存在形如 $(i, i+1)$ 的边（$1 \le i \le k$），且仅有这些边。特别地，仅含一个顶点的图视为长度为 $0$ 的链。收缩操作中新生成的顶点也可以参与进一步的收缩。 如下图所示，红色标记的两个点发生了收缩操作。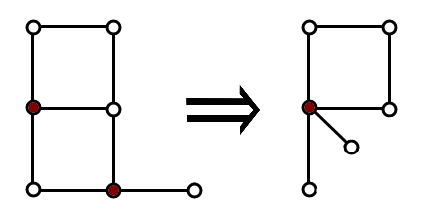  请你帮助 Vova 找出最终可以得到的链的最大长度，或者判断无法获得链。

第一行包含两个整数 $n, m$（$1 \le n \le 1000$，$0 \le m \le 100000$），表示原图的顶点数和边数。 接下来的 $m$ 行，每行包含两个整数 $a_i, b_i$（$1 \le a_i, b_i \le n$，$a_i \ne b_i$），表示一条连接顶点 $a_i$ 和 $b_i$ 的无向边。保证任意一对顶点之间至多存在一条边。

如果无法将给定图变为链，输出 $-1$。否则输出最终链中可能的最大边数。

在第一个样例中，你可以对顶点 $4$ 和 $5$ 进行收缩操作，得到一条长度为 $3$ 的链。 在第二个样例中，最初无法对任意两个顶点进行收缩，无法得到链。 在第三个样例中，你可以对顶点 $1$ 和 $2$ 进行收缩，得到一条长度为 $2$ 的链。 由 ChatGPT 5 翻译