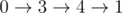CF547A Mike and Frog

Mike has a frog and a flower. His frog is named Xaniar and his flower is named Abol. Initially(at time $0$ ), height of Xaniar is $h_{1}$ and height of Abol is $h_{2}$ . Each second, Mike waters Abol and Xaniar. So, if height of Xaniar is $h_{1}$ and height of Abol is $h_{2}$ , after one second height of Xaniar will become 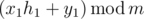 and height of Abol will become 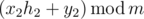 where $x_{1},y_{1},x_{2}$ and $y_{2}$ are some integer numbers and 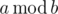 denotes the remainder of $a$ modulo $b$ . Mike is a competitive programmer fan. He wants to know the minimum time it takes until height of Xania is $a_{1}$ and height of Abol is $a_{2}$ . Mike has asked you for your help. Calculate the minimum time or say it will never happen.

The first line of input contains integer $m$ ( $2 \le m \le 10^{6}$ ). The second line of input contains integers $h_{1}$ and $a_{1}$ ( $0 \le h_{1},a_{1}

Print the minimum number of seconds until Xaniar reaches height $a_{1}$ and Abol reaches height $a_{2}$ or print -1 otherwise.

In the first sample, heights sequences are following: Xaniar:  Abol: