CF549H Degenerate Matrix
题目描述
$2 \times 2$ 矩阵的行列式定义如下:
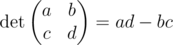
如果一个矩阵的行列式等于零,则称该矩阵为退化矩阵。
矩阵 $A$ 的范数 $||A||$ 被定义为其各元素绝对值的最大值。
给定矩阵 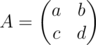,请你考虑任意一个范数 $||A-B||$ 最小的退化矩阵 $B$,求 $||A-B||$ 的最小值。
输入格式
第一行包含两个整数 $a$ 和 $b$($|a|, |b| \leq 10^{9}$),表示矩阵 $A$ 的第一行元素。
第二行包含两个整数 $c$ 和 $d$($|c|, |d| \leq 10^{9}$),表示矩阵 $A$ 的第二行元素。
输出格式
输出一个实数,表示 $||A-B||$ 的最小可能值。只要你的答案与标准答案的绝对误差或相对误差不超过 $10^{-9}$,就会被判定为正确。
说明/提示
在第一个样例中,矩阵 $B$ 是 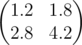。
在第二个样例中,矩阵 $B$ 是 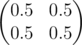。
由 ChatGPT 5 翻译