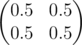CF549H Degenerate Matrix

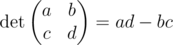The determinant of a matrix $ 2×2 $ is defined as follows: A matrix is called degenerate if its determinant is equal to zero. The norm $ ||A|| $ of a matrix $ A $ is defined as a maximum of absolute values of its elements. You are given a matrix 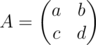. Consider any degenerate matrix $ B $ such that norm $ ||A-B|| $ is minimum possible. Determine $ ||A-B|| $ .

The first line contains two integers $ a $ and $ b $ ( $ |a|,|b|

Output a single real number, the minimum possible value of $ ||A-B|| $ . Your answer is considered to be correct if its absolute or relative error does not exceed $ 10^{-9} $ .

In the first sample matrix $ B $ is 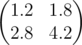 In the second sample matrix $ B $ is