CF551D GukiZ and Binary Operations

We all know that GukiZ often plays with arrays. Now he is thinking about this problem: how many arrays $ a $ , of length $ n $ , with non-negative elements strictly less then $ 2^{l} $ meet the following condition: 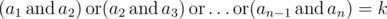? Here operation 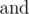 means bitwise AND (in Pascal it is equivalent to and, in C/C++/Java/Python it is equivalent to &), operation 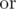 means bitwise OR (in Pascal it is equivalent to 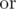, in C/C++/Java/Python it is equivalent to |). Because the answer can be quite large, calculate it modulo $ m $ . This time GukiZ hasn't come up with solution, and needs you to help him!

First and the only line of input contains four integers $ n $ , $ k $ , $ l $ , $ m $ ( $ 2

In the single line print the number of arrays satisfying the condition above modulo $ m $ .

In the first sample, satisfying arrays are $ {1,1},{3,1},{1,3} $ . In the second sample, only satisfying array is $ {1,1} $ . In the third sample, satisfying arrays are $ {0,3,3},{1,3,2},{1,3,3},{2,3,1},{2,3,3},{3,3,0},{3,3,1},{3,3,2},{3,3,3} $ .