CF557E Ann and Half-Palindrome

Tomorrow Ann takes the hardest exam of programming where she should get an excellent mark. On the last theoretical class the teacher introduced the notion of a half-palindrome. String $ t $ is a half-palindrome, if for all the odd positions $ i $ (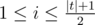) the following condition is held: $ t_{i}=t_{|t|-i+1} $ , where $ |t| $ is the length of string $ t $ if positions are indexed from $ 1 $ . For example, strings "abaa", "a", "bb", "abbbaa" are half-palindromes and strings "ab", "bba" and "aaabaa" are not. Ann knows that on the exam she will get string $ s $ , consisting only of letters a and b, and number $ k $ . To get an excellent mark she has to find the $ k $ -th in the lexicographical order string among all substrings of $ s $ that are half-palyndromes. Note that each substring in this order is considered as many times as many times it occurs in $ s $ . The teachers guarantees that the given number $ k $ doesn't exceed the number of substrings of the given string that are half-palindromes. Can you cope with this problem?

The first line of the input contains string $ s $ ( $ 1

Print a substring of the given string that is the $ k $ -th in the lexicographical order of all substrings of the given string that are half-palindromes.

By definition, string $ a=a_{1}a_{2}...\ a_{n} $ is lexicographically less than string $ b=b_{1}b_{2}...\ b_{m} $ , if either $ a $ is a prefix of $ b $ and doesn't coincide with $ b $ , or there exists such $ i $ , that $ a_{1}=b_{1},a_{2}=b_{2},...\ a_{i-1}=b_{i-1},a_{i}<b_{i} $ . In the first sample half-palindrome substrings are the following strings — a, a, a, a, aa, aba, abaa, abba, abbabaa, b, b, b, b, baab, bab, bb, bbab, bbabaab (the list is given in the lexicographical order).