CF570E Pig and Palindromes

小猪佩奇在散步时误入了一片森林。真是太巧了！这片森林呈现矩形的形状，共有 $n$ 行 $m$ 列。我们从上到下依次用 $1$ 到 $n$ 标记各行，从左到右依次用 $1$ 到 $m$ 标记各列。我们用 $(r,c)$ 表示第 $r$ 行第 $c$ 列的格子。 最开始，小猪站在格子 $(1,1)$，她最终想走到格子 $(n,m)$。由于她急着回家，每一步她只能从格子 $(r,c)$ 走到 $(r+1,c)$ 或 $(r,c+1)$。她不能离开这片森林。 这片森林非常特殊。有些格子相似，有些则完全不同。佩奇喜欢拍照，她每移动一次就会对当前所在的格子拍一张照。如果从 $(1,1)$ 到 $(n,m)$ 的整条路径上，每一步格子拍下的照片序列，正着看和反着看都是一样的（即该序列为回文串），那么就称这是一条美丽的路径（"beautiful path"）。也就是说，按顺序访问的格子的所有编号形成的序列需要是回文序列。 计算从 $(1,1)$ 到 $(n,m)$ 遍历所有美丽路径的总数。由于答案可能很大，请输出对 $10^9 + 7$ 取模的结果。

第一行包含两个整数 $n,m$（$1 \leq n, m \leq 500$），表示丛林的高度和宽度。 接下来 $n$ 行，每行包含 $m$ 个小写英文字母，表示森林中各个格子的类型。相同类型的格子用相同的字母，不同类型的格子用不同的字母表示。

输出一个整数，表示美丽路径的数量，对 $10^9+7$ 取模。

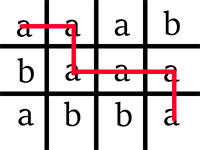
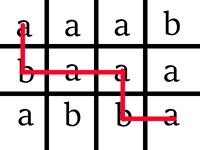
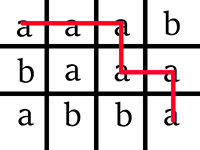
下图展示了样例测试可能的路径。    由 ChatGPT 5 翻译