CF575A Fibonotci
Description
Fibonotci sequence is an integer recursive sequence defined by the recurrence relation
$ F_{n}=s_{n-1}·F_{n-1}+s_{n-2}·F_{n-2} $ with $ F_{0}=0,F_{1}=1 $ Sequence $ s $ is an infinite and almost cyclic sequence with a cycle of length $ N $ . A sequence $ s $ is called almost cyclic with a cycle of length $ N $ if 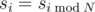, for $ i>=N $ , except for a finite number of values $ s_{i} $ , for which 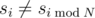 ( $ i>=N $ ).
Following is an example of an almost cyclic sequence with a cycle of length 4:
s = (5,3,8,11,5,3,7,11,5,3,8,11,…) Notice that the only value of $ s $ for which the equality 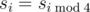 does not hold is $ s_{6} $ ( $ s_{6}=7 $ and $ s_{2}=8 $ ). You are given $ s_{0},s_{1},...s_{N-1} $ and all the values of sequence $ s $ for which 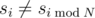 ( $ i>=N $ ).
Find 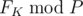.
Input Format
The first line contains two numbers $ K $ and $ P $ . The second line contains a single number $ N $ . The third line contains $ N $ numbers separated by spaces, that represent the first $ N $ numbers of the sequence $ s $ . The fourth line contains a single number $ M $ , the number of values of sequence $ s $ for which 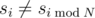. Each of the following $ M $ lines contains two numbers $ j $ and $ v $ , indicating that 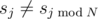 and $ s_{j}=v $ . All j-s are distinct.
- $ 1
Output Format
Output should contain a single integer equal to 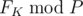.