CF575H Bots

Sasha 和 Ira 是两位最好的朋友。但她们不仅是朋友，还是软件工程师，并且是人工智能领域的专家。她们正在为两个机器人玩二人合作、回合制游戏开发一个算法。每一回合，由其中一名玩家进行一次操作（哪位玩家进行操作并不重要，玩家的出手可不必交替进行）。 Sasha 和 Ira 开发的机器人算法通过追踪游戏当前的状态来运作。每当任一机器人进行一次操作时，游戏的状态就会发生变化。而且由于游戏非常动态，任何时刻游戏都不会回到曾经出现过的状态。 Sasha 和 Ira 是完美主义者，她们希望算法能有最优的获胜策略。她们注意到，在最优获胜策略下，两位机器人分别恰好各进行 $N$ 次操作。但是，为了找到最优策略，她们的算法需要分析游戏的所有可能状态（她们还没有学到 alpha-beta 剪枝）并选择最佳的操作序列。 她们担忧算法的效率，并想知道总共需要分析多少种可能的游戏状态？

第一行包含一个整数 $N$。 - $1 \leq N \leq 10^6$

输出一个整数，表示可能的游戏状态数，对 $10^9+7$ 取模。

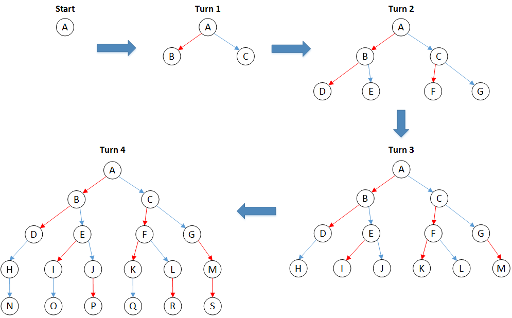
初始时游戏处于状态 A。 - 第 1 步：任意一名机器人可以进行一次操作（第一名为红色机器人，第二名为蓝色机器人），因此在第一步后可能出现两种状态——B 和 C。 - 第 2 步：在状态 B 和状态 C 下，任意一名机器人都可以继续出手，因此可能出现状态 D、E、F 和 G。 - 第 3 步：在状态 D 时红色机器人已做了 $N=2$ 次操作，不能再操作。在状态 E、F、G 时红色机器人还能操作，于是状态 I、K、M 被加入。同理，蓝色机器人在状态 G 时已做了 2 次操作，不能再操作，但在状态 D、E、F 时还能操作，于是状态 H、J、L 被加入。 - 第 4 步：在状态 H、I、K 时红色机器人已做了 $N=2$ 次操作，只能在 J、L、M 时操作，于是状态 P、R、S 被加入。蓝色机器人在 J、L、M 时已做了 2 次操作，不能再操作，只能在 H、I、K 时操作，于是状态 N、O、Q 被加入。 最终，她们的算法需要分析 19 种可能的游戏状态。  由 ChatGPT 5 翻译