CF576C Points on Plane

On a plane are $ n $ points ( $ x_{i} $ , $ y_{i} $ ) with integer coordinates between $ 0 $ and $ 10^{6} $ . The distance between the two points with numbers $ a $ and $ b $ is said to be the following value: 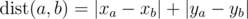 (the distance calculated by such formula is called Manhattan distance). We call a hamiltonian path to be some permutation $ p_{i} $ of numbers from $ 1 $ to $ n $ . We say that the length of this path is value 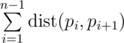. Find some hamiltonian path with a length of no more than $ 25×10^{8} $ . Note that you do not have to minimize the path length.

The first line contains integer $ n $ ( $ 1

Print the permutation of numbers $ p_{i} $ from $ 1 $ to $ n $ — the sought Hamiltonian path. The permutation must meet the inequality 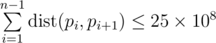. If there are multiple possible answers, print any of them. It is guaranteed that the answer exists.

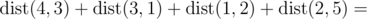
In the sample test the total distance is:  $ (|5-3|+|0-4|)+(|3-0|+|4-7|)+(|0-8|+|7-10|)+(|8-9|+|10-12|)=2+4+3+3+8+3+1+2=26 $